Seguramente en clase el profesor te ha arruinado tu fin de semana enviándote tareas para el hogar. Es probable que hoy te inviten a una fiesta súper genial con tus amigos pero, por tus prioridades académicas, no tengas el tiempo suficiente para relajarte sin preocupaciones.
Por esto, hoy te enseñaré qué es un múltiplo y lo procedimientos llevados a cabo para obtenerlo. Seré breve, fluido y cuidadoso en no malgastar tu tiempo. Las matemáticas pueden ser muy complejas, mas son entendibles fácilmente cuando se les pone atención. Esa puede ser la razón del ¿por qué la libreta de matemáticas siempre es roca?
¿Qué es un múltiplo?
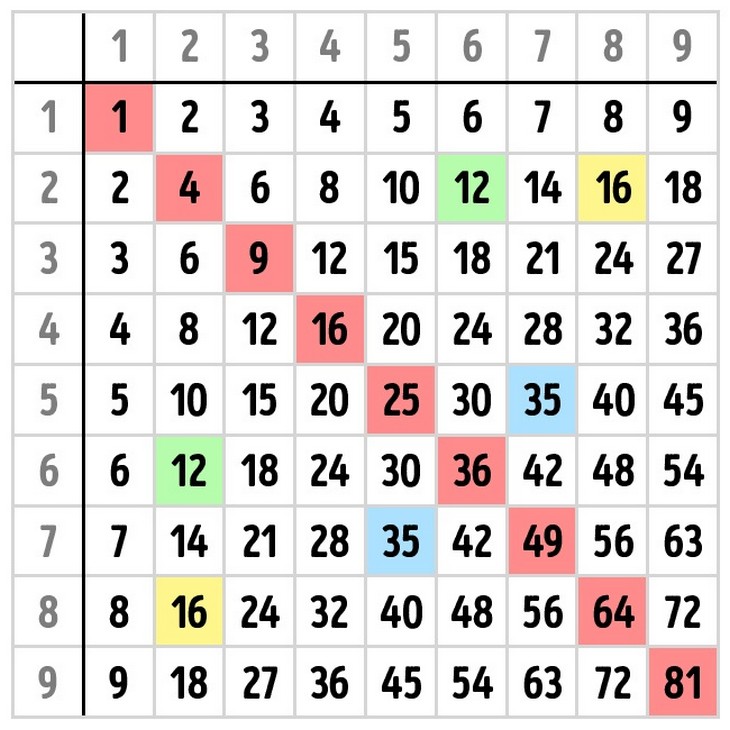
Para ser exactos, un múltiplo es el resultado de toda multiplicación. Cuando te pregunten cómo sacarle el múltiplo a un número siempre deberás recurrir a la multiplicación del mismo por otros dígitos; ejemplo:
3×1= 3, 3×2= 6, 3×3= 9, 3×4= 12, 3×5= 15…
En este caso, los múltiplos del número 3 son: 3, 6, 9, 12 y 15.
Y habrás notado que aún puedes seguir multiplicando hasta el infinito y más allá; te explico, se pueden obtener múltiplos infinitamente de un solo número. Imagínate si por no realizar tus tareas fueses condenado a pasar la eternidad sacando los múltiplos de cada número, ¡qué infierno matemático! Pero no te preocupes porque hay trucos para aprender matemáticas con Lego.
El múltiplo común
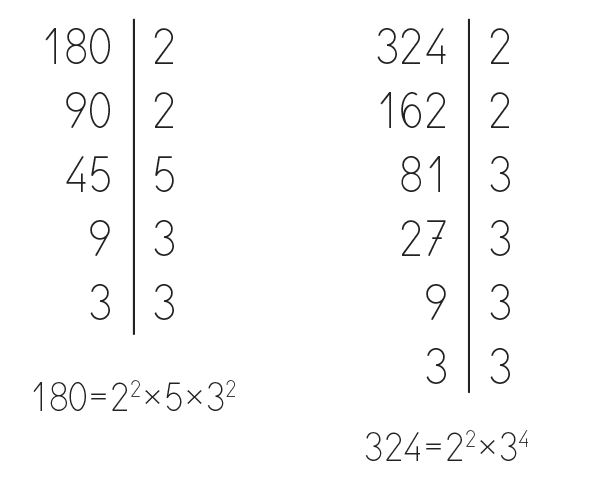
Prosiguiendo con las operaciones, ahora te hablaré de un término derivado de la explicación anterior: múltiplo común. Ya sabes que el múltiplo por sí sólo es el simple resultado de multiplicar un número natural con cualquier otro; del mismo modo, los múltiplos de varios dígitos pueden ser comunes.
2×3= 6, 2×6= 12, 2×9= 18.
3×2= 6, 3×4= 12, 3×6= 18.
Aquí puedes examinar que los múltiplos comunes del número 3 y el número 2 son: 6, 12 y 18.
En cuanto a las fórmulas que omití, podrás intuir que los resultados no poseen una semejanza natural:
2×1= 2, 2×2= 4, 2×5= 10, 2×7= 14, 2×8= 16, 2×10= 20.
3×1= 3, 3×3= 9, 3×5= 15, 3×7= 21, 3×8= 24, 3×10= 30.
¿Ya lo viste? Estas fórmulas no tienen nada en común. Sin embargo, te servirán para discernir cuáles son múltiplos comunes entre ambos o más dígitos.
Mínimo común múltiplo
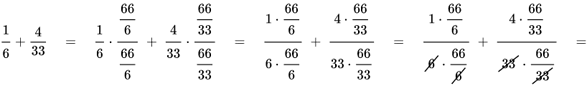
La siguiente ramificación es el mínimo común múltiplo (MCM); también muy fácil de entender. Para saber dónde aplicar dicho término debes redirigirte al inicio de las filas y marcar uno por uno los múltiplos comunes. Cuando lo hayas hecho, sabrás que el mínimo común múltiplo será el de menor denominación numérica.
Múltiplos del 4= 4, 8, 12, 16, (20), 24, 28, 32, 36, 40.
Múltiplos del 2= 2, 4, 6, 8, 10, 12, 14, 16, 18, (20).
Múltiplos del 10= 10, (20), 30, 40, 50, 60, 70, 80, 90, 100.
Encerrados entre paréntesis están los mínimos común múltiplo de 4, 2 y 10. A pesar de que 12 y 16 también son múltiplos comunes entre 4 y 2, no pueden ser el mínimo porqué no aparecen en la fila del tercer candidato. Lo que da como resultado que 20 es el sujeto que buscabas.
Pero en un caso distinto, donde haya más de un MCM, por obligación lógica siempre deberás elegir el de menor valor.
Múltiplos del 6= 6, 12, 18, (24), 30, 36, 42, (48), 54, 60, 66, (72).
Múltiplos del 8= 8, 16, (24), 32, 40, (48), 56, 64, (72), 80.
En el ejemplo de arriba hay tres MCM entre paréntesis: 24, 48 y 72. Pero tu resultado jamás podrán ser todos mientras que el profesor no te lo indiqué como parte del ejercicio. Será únicamente la cifra 24, pues, es la de menor valor y representa la connotación gramatical del mínimo común múltiplo.
El divisor
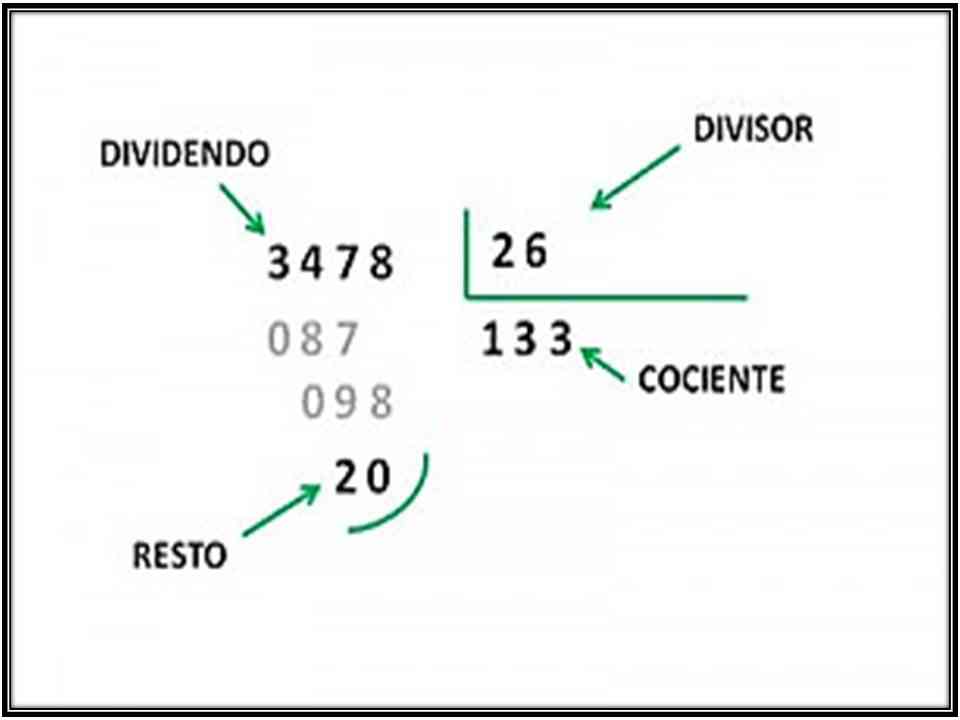
Al igual que los múltiplos, los divisores son un recurso fundamental para tus conocimientos matemáticos. Tal vez sientas confusión cuando oigas, por primera vez, a tu profesor decir: “Chicos, ¿quién sabe cuál es el divisor del número 8? Pero a continuación te enseñaré cómo responderle.
12÷6= 2, 8÷2=4, 18÷9= 2.
En esencia, un número es divisor de otro cuando la división entre ambos te da una cifra exacta. Puedes observar que los ejemplos de arriba soltaron el producto que deseamos. El número divisor de 12, es 6; el de 18, 9 y, finalmente, el de 8 es 2. De modo que…
5÷4= 1.25, 25÷6= 4.16, 10÷9= 1.11.
No debes considerarlas como operaciones con números divisores. Los divisores tienen la capacidad de segregarse, en partes iguales, al derecho y al revés.
21÷7= 3 o, también, 21÷3= 7.
Números primos y compuestos
Ahora que entiendes que son los divisores y, los múltiplos, con sus derivados, te mostraré qué es número primo y uno compuesto. Un número primo es aquella cifra natural que sólo puede dividirse consiga misma y el divisor uno. O sea, estos números no tienen par ni puede sacarse de ellos una división exacta en mitades.
2÷1= 2, 2÷2= 1, 3÷1= 3, 3÷3= 1, 5÷5= 1, 5÷1= 5.
Los primeros números del orden infinito tienden a ser primos: 2, 3, 5, 7, 9, 11, 13, 17.
Mientras que los números compuestos son los que pueden dividirse por más de un divisor, dándote mitades perfectamente equilibradas. Por ejemplo:
4, 6, 8, 10, 12, 14, 15, 16.
En cambio el número 1 es una excepción indefinible, no es primo ni es compuesto. Ya que los dígitos primarios sólo puedes dividirlos dos veces; y, de los compuestos, resultan dígitos recíprocamente divisibles. Se definiría, en conclusión, como una unidad capaz de dividir a todos los demás números.
