El radian es una medida que corresponde a la unidad de ángulo dentro del sistema internacional de medidas. Esta unidad derivada tiene la función de determinar el número de veces que cabe en el arco de una circunferencia, dando a entender también la medida exacta de la longitud de dicho radio.
¿Por qué es importante?

Esta medida es sumamente útil para la medición de ángulos, simplificando todas las expresiones de cálculo ya que se usarían únicamente múltiplos sencillos, o de igual manera, divisores de radianes, los cuales son representados por el número π.
El radian es un término muy usado en algunas materias referentes a física, cálculo infinitesimal o trigonometría, y algunas otras materias similares, es por ello que se debe conocer todo sobre qué es y cómo funciona.
Grados a radianes

Hay una equivalencia entre radianes y grados que es bastante útil de conocer para de esta forma simplificar términos en operaciones de cualquier tipo naturaleza. Para las operaciones con radianes se usan con más frecuencia los grados sexagesimales y centesimales:
La equivalencia que existe entre grados sexagesimales y radianes es: π rad = 180º, por lo que entonces:
1 grado sexagesimal equivale a 0,01745329252… radianes.
1 radián equivale a 57,2958… grados sexagesimales.
Por otra parte, la equivalencia entre grados centesimales y radianes es: π rad = 200g.
1 grado centesimal equivale a 0.015708… radianes
1 radian equivale a 63,662… grados centesimales.
Como se puede apreciar, tanto grados como los radianes son dos unidades de medida bastante diferentes, pero que en cualquier caso ambas se usan por igual en el momento de representar o hacer las mediciones de cualquier clase de ángulo, por lo tanto existen ente algunas semejanzas como lo es la búsqueda de la simplificación de los términos al seguir algunas reglas que han de hacerse de forma correcta para así obtener una conversión coherente.
Por ende, es posible decir que si se necesita transformar los radianes a grados o grados a radianes, lo que puedes hacer, como una alternativa mucho menos complicada, es usar una sencilla regla de tres a partir del principio de que π es equivalente a 180 º.
Grados y radianes
Ahora, para transformar los radianes a grados, y viceversa, solo tendrás que hacer los siguientes cálculos:
De grados a radianes: Para esto vas a tener que multiplicar el ángulo por π/180 y simplificar el resultado. Si quieres descubrir cómo hacerlo, solo deberás seguir estas indicaciones:
- En primer lugar debes multiplicar el ángulo por π/180.
- Después elimina los grados del resultado.
- Luego, reduce la fracción a su mínima expresión.
- Y finalmente obtendrás el resultado.
De radianes a grados: Pero si necesitas pasar los radianes a grados, tendrás que multiplicar la cantidad de estos por 180°/π. Para ello sigue estas indicaciones.
- Una vez tengas la cantidad de radianes que necesites transformar, tendrás que multiplicarlos por 180°/π.
- Después debes eliminar los términos semejantes.
- Para finalizar dolo deberás reducir el resultado a su mínima expresión.
Ángulos a radianes y cuadrantes
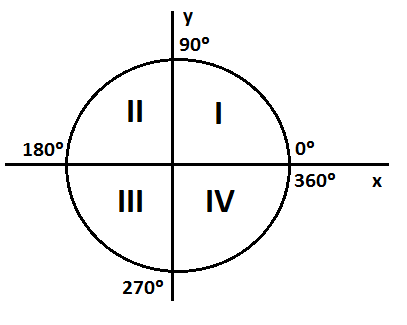
Una circunferencia, en trigonometría puede dividirse en 4 partes, las cuales tienen el nombre de cuadrantes. Estos cuadrantes están delimitados por los llamados ejes de coordenadas.
Una manera para dividir o numerar una circunferencia es utilizando los radianes. Ya que un radian equivale a la medida que tiene el ángulo central, cuyo arco mide lo mismo que el radio. En otras palabras, se puede decir que en este caso, un radian es cuando tomas la distancian que hay entre el eje central de la circunferencia y la línea de esta, con la intensión de medir la cantidad de veces que caben dentro de dicha circunferencia.
Un ejemplo es que, si existe una distancia de 10cm entre el eje central y la línea de circunferencia, deberás medir la cantidad de veces que se repite esta medida en toda la línea de circunferencia.
Para ello, en caso de representar las medidas de los ángulos en radianes, se puede decir que si la circunferencia es L (circunferencia)=2 x π x r (radio):
- El ángulo completo equivale a 2π.
- En un ángulo llano se tienen π radianes.
- Y en un solo ángulo recto hay π/2 radianes.
De esta forma puedes comprender que la circunferencia mide exactamente 2π y que al representarlo en grados se obtiene un total de 360°. De esta forma habrás hecho una conversión de grados a radianes al simplificar términos y hacer más entendible el proceso junto a las cifras finales
Conversión de ángulos más comunes
Grados – Radianes
0º 0
30º π/6
45º π/4
60º π/3
90º π/2
120º 2π/3
135º 3π/4
150º 5π/6
180º π
210º 7π/6
225º 5π/4
240º 4π/3
270º 3π/2
300º 5π/3
315º 7π/4
330º 11π/6
360º 2π
