A diferencia de la esfera o el cilindro, un prisma, por definición, no es un cuerpo claramente definido en geometría. Más bien, un prisma se puede describir como un grupo o tipo de cuerpos geométricos, cuya base es cualquier polígono (por ejemplo, triángulo, hexágono).
Todos los bordes laterales son paralelos entre sí y de la misma longitud. Por tanto, la zona de la base y la zona superior son idénticas.
PRISMA
Como ocurre con todos los cuerpos geométricos, podemos diferenciar entre la base, la parte superior y la superficie lateral de un prisma. La siguiente figura muestra dos prismas ejemplares. La base o superficie superior del prisma izquierdo es un triángulo. La superficie exterior consta de tres rectángulos.
Cuando abre la superficie exterior, estos tres rectángulos juntos forman un rectángulo grande. La base o superficie superior del prisma derecho es un hexágono. El abrigo consta de seis rectángulos. Cuando abre la superficie exterior, estos seis rectángulos juntos también dan como resultado un rectángulo grande.
La superficie exterior de un prisma es siempre un rectángulo, independientemente de la forma de la base.
Si el desplazamiento paralelo tiene lugar perpendicular a la superficie dada, se habla de un prisma recto, en caso contrario de un prisma torcido. El polígono dado se llama base, la otra superficie límite congruente y paralelo se llama superficie superior.
La totalidad de todas las demás superficies de contorno se llama chaqueta. Consiste en paralelogramos, en el caso especial del prisma recto de los rectángulos.
- El prisma cumple con la definición general de cilindro.
- El cuboide es una forma especial del prisma. Visto desde cada lado, es un prisma.
- En el sentido más estricto, en óptica, un prisma generalmente se entiende como un prisma recto con un triángulo como base, ver prisma (óptica).
El volumen V de un prisma viene dado por:
V = AG ⋅ h,
Donde AG es el área de la base y h es la altura del prisma.
La superficie exterior AM de un prisma recto viene dada por
AM = UG ⋅ h,
Donde UG representa la circunferencia de la base y h la altura del prisma. Esta fórmula no es correcta para prismas torcidos.
Toda la superficie O de un prisma resulta de
O = 2 ⋅ AG + AM,
Donde AG y AM corresponden al contenido de la base y el área de la superficie.
PRISMAS CON ESFERA INC
Para prismas rectos que tienen una esfera inclinada, se aplica lo siguiente:
AM = 4 ⋅ AG
Hechos y fórmulas sobre el prisma.
Ya hemos enumerado las cosas más importantes sobre el cuerpo geométrico, el prisma:
MÉTODO
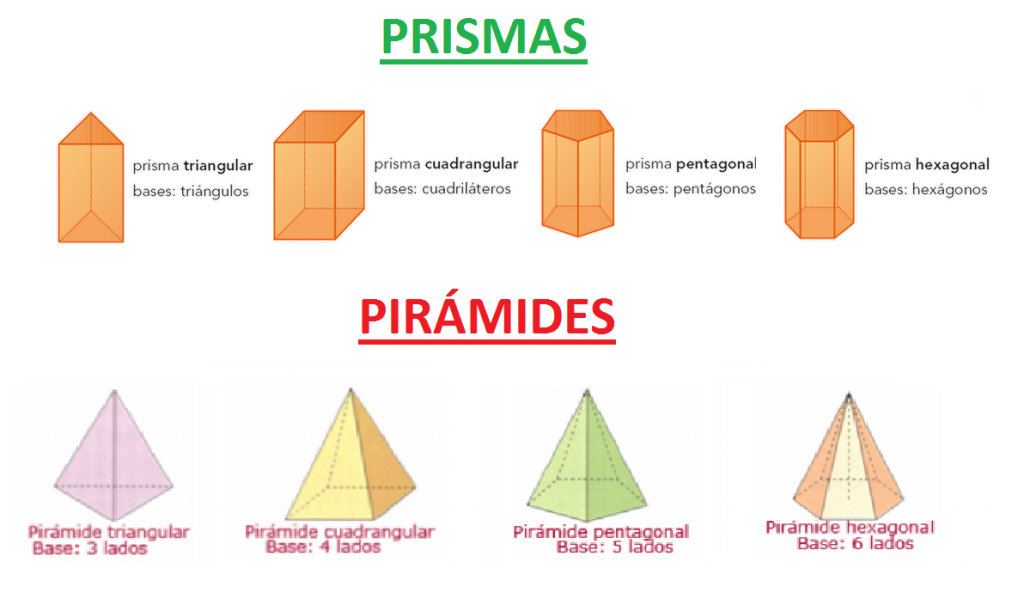
Las áreas de la base de los prismas pueden verse diferentes. El área de la base puede ser, por ejemplo, un triángulo ("prisma triangular") o un hexágono ("prisma hexagonal").
Puedes calcular el volumen de un prisma usando la fórmula VPrisma = G ⋅ h. La fórmula del área de la base G varía según la forma del área de la base.
Calcula la superficie de un prisma usando la fórmula AG = U⋅h prisma. Aquí varían tanto la fórmula del área del área base como la del área lateral.
QUÉ ES UN PRISMA: DEFINICIÓN
A diferencia de la esfera o el cilindro, un prisma, por definición, no es un cuerpo claramente definido en geometría. Más bien, un prisma se puede describir como un grupo o tipo de cuerpos geométricos, cuya base es cualquier polígono (por ejemplo, triángulo, hexágono).
Todos los bordes laterales son paralelos entre sí y de la misma longitud. Por tanto, la zona de la base y la zona superior son idénticas.
Como ocurre con todos los cuerpos geométricos, podemos diferenciar entre la base, la parte superior y la superficie lateral de un prisma. La siguiente figura muestra dos prismas ejemplares. La base o superficie superior del prisma izquierdo es un triángulo.
superficie exterior consta de tres rectángulos. Cuando abre la superficie exterior, estos tres rectángulos juntos forman un rectángulo grande.
La base o superficie superior del prisma derecho es un hexágono. El abrigo consta de seis rectángulos. Si abres la superficie exterior, estos seis rectángulos juntos también dan como resultado un rectángulo grande. La superficie exterior de un prisma es siempre un rectángulo, independientemente de la forma de la base.
¿Cómo se calcula el volumen de un prisma?
Dado que un prisma puede adoptar diferentes formas dependiendo de su base, no podemos dar una fórmula de prisma específica y generalmente válida para calcular el volumen.
Sin embargo, podemos dar una fórmula para calcular el volumen, aunque relativamente general. (Esta fórmula de prisma es similar a las fórmulas para calcular el volumen de un cuboide o un cubo).
NOTA
- VPrisma = G ⋅ h
- G = área de la base
- h = altura del prisma
Dado que la forma de la base es variable, no podemos encontrar una fórmula más específica.
¿Cómo se calcula la superficie de un prisma?
Incluso con la superficie o el área de la superficie, solo podemos establecer una fórmula de prisma muy general. La superficie de un prisma está formada por el área de la superficie superior, base y exterior.
Dependiendo de la forma de la base del prisma, debes encontrar la fórmula correcta del prisma para el polígono correspondiente.
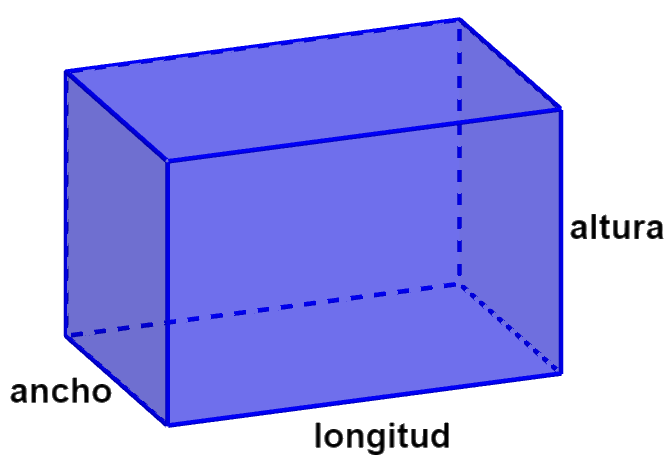
La superficie exterior de un prisma es siempre un rectángulo. Se conocen las dos longitudes de los lados de este rectángulo: la longitud de un lado del rectángulo corresponde a la circunferencia del área de la base (área de la base en U) y la longitud del otro lado corresponde a la altura del prisma (hprisma).