El mundo comienza en un punto; en el Big Bang, un punto infinitamente pequeño de densidad infinita. El punto es el inicio de la pintura y el marco de las oraciones, regula el lenguaje y marca las dimensiones.
El punto es la forma más pequeña, la aparición más breve en términos de tiempo. El punto es el remanente de lo que fue pasado y el material del que emergen las cosas nuevas.
La creación de un orden (es) más fácil (…) que la creación de un desorden, un informe”- Frutiger 1978.
PUNTO GEOMÉTRICO
- Ser inmaterial
- Símbolo de cero
- Intersección
- Punto de impacto
- Marcos
- Marcado dimensional (definición de una posición en una línea, plano, espacio, tiempo…)
Percepción
El punto es un contraste complementario
- Materia – vacío
- Marcado – espacio
- Blanco y negro
- Objeto – medio ambiente
El punto marca el espacio y, por tanto, es información. Sin embargo, uno especial, ya que no tiene límite. Cf. teoría de sistemas: según George Spencer Brown, la información es una marca que crea una triplicidad a través de su dualidad: la marcación de un «interior» crea un «exterior» y, por tanto, también un «límite». El límite del punto, sin embargo, es su interior.
PUNTO GEOMÉTRICO
Un punto es un elemento de geometría y, de manera simplificada, representa un área circular, sin embargo, el punto geométrico no tiene extensión, el radio es 0. El punto es el componente más pequeño de la geometría.
Puedes armar todo con él. Si colocas muchos puntos seguidos, obtienes una línea. Si colocas los muchos puntos no solo uno detrás del otro, sino también uno al lado del otro, obtienes un área. Si también pones los muchos puntos uno encima del otro, obtienes un cuerpo.
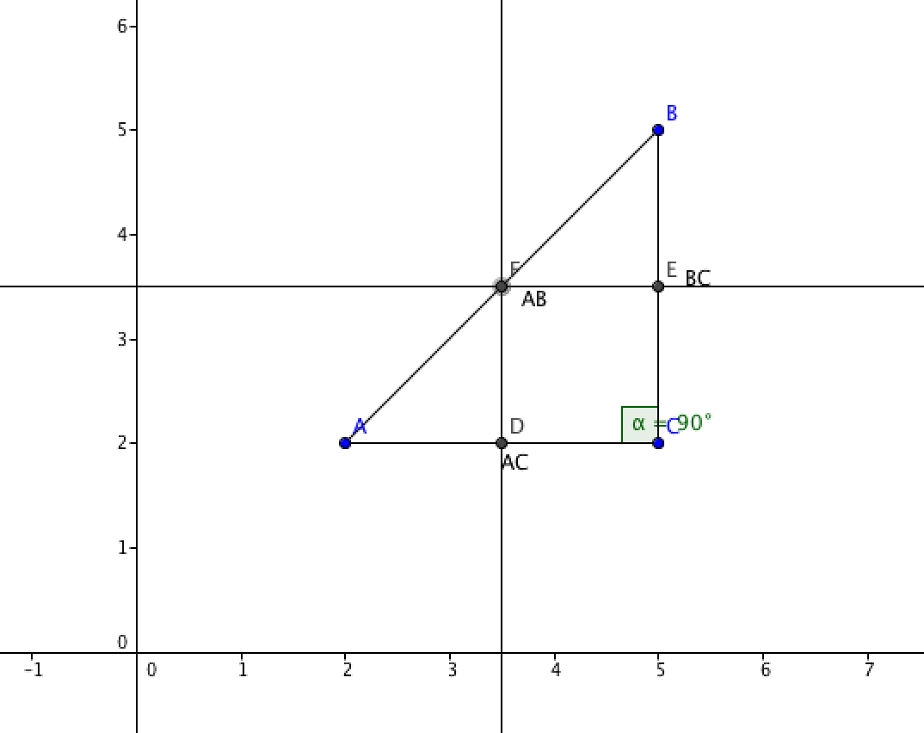
Sin embargo, los puntos también tienen una posición en la que se encuentran. Para ello necesita un sistema de coordenadas. Se trata de una cuadrícula que consta de dos ejes que giran 90 °.

Un eje es horizontal y se llama eje X. Determina la dirección horizontal (izquierda / derecha). El otro eje es vertical y se llama eje Y. Determina la dirección vertical (arriba / abajo).
RESUMEN
Un punto no tiene partes y una línea o recta está dada por puntos, al menos según el antiguo matemático Euclides.
E incluso hoy se dice que un punto no tiene extensión. ¿No contradice eso todas las experiencias basadas en la intuición sensual? Algo que no tiene expansión no puede ser divisible, ¿verdad? Me pregunto por qué, después de todo, un punto físico-empírico en el espacio es divisible y si es finito o infinitamente divisible. La contradicción se ha planteado muchas veces, ya en el siglo V a. C.
El alumno de Parménides, Zenón, estableció varias paradojas, la más famosa de las cuales es la de Aquiles y la tortuga. Zenón sostiene que el más rápido (Aquiles) nunca alcanzaría al más lento (la tortuga).
Porque el perseguidor (Aquiles) siempre tiene que llegar donde ya se fue la tortuga. Por lo tanto, se tendría que cubrir un número infinito de secciones, por lo que Aquiles nunca alcanza a la tortuga porque el cable se hace cada vez más pequeño, pero nunca puede detenerse. Zenón muestra que esta divisibilidad infinita conduce a un resultado paradójico.
Punto
Concepto básico de geometría, cuyo contenido está determinado por los axiomas de la geometría.
Dado que se trata de un término básico, la definición del término “punto” no es posible, aunque se ha intentado durante mucho tiempo darle definiciones coherentes. Entonces Euclides dio la siguiente definición en sus «Elementos»:
Un punto es lo que no tiene partes.
Sin embargo, esta definición no hace ninguna declaración, ya que la propiedad descriptiva “no tener partes” no está definida en sí misma.
Los puntos tienen algunas peculiaridades en las que no siempre piensas. Son objeto de las siguientes consideraciones. Espero algunas contradicciones.
Si dibujas un punto en un papel o en la pizarra, en realidad obtendrá un área pequeña o un pequeño «montón de tiza». Los puntos son cosas del pensamiento y no se pueden ver ni dibujar. A veces se les llama «infinitamente pequeños».
Euclides dice: «Un punto es aquello que no tiene partes». Para comprender mejor lo que significa esto, comencemos con algo más grande y manejable, una superficie o un cuerpo.
Los dividimos continuamente, primero físicamente, luego solo en el pensamiento. Con Euclides este proceso de división llega a su fin, porque cuando dice que el punto no tiene partes, según esta concepción debe haber algo muy pequeño que no se pueda desglosar más.
Atómo de geometría
Un «átomo de geometría», por así decirlo, del griego átomos = indivisible, similar al de la física y la química, donde el término átomo, que se originó en la antigüedad, ya no es apropiado y solo se retiene de la tradición.
Según Euclides, me parece que un punto es algo muy pequeño, pero conserva un tamaño finito. Donde yace permanece abierto.
Lo contrario es que el proceso de división continúa sin llegar nunca a un límite. Entonces el punto adquiere carácter asintótico. Quien dice que un punto es infinitamente pequeño no se refiere a un objeto fijo, sino a uno que todavía está en proceso de devenir. Estrictamente hablando, no debería haber ningún punto «terminado».
Aunque los puntos y los números inicialmente no tienen nada que ver entre sí, se establece una conexión entre ellos marcando ciertos puntos con números en una línea recta o segmento. Esto sucede primero con los números naturales; luego se suman el cero y los números enteros negativos.
Los puntos dentro de los intervalos entre dos números enteros también se pueden marcar de esta manera: el punto correspondiente a la fracción 51/3 = 16/3, por ejemplo, encuentra su lugar en la recta numérica como cualquier otro punto perteneciente a un número racional m / n, donde myn son números enteros (n distintos de cero). También se habla brevemente de «puntos racionales».
