En la geometría, la apotema es la línea que conecta el centro de un polígono regular con el punto medio de uno de sus lados.
Para entender mejor está definición necesitamos saber ¿Que es un polígono regular?
En matemáticas, un polígono regular es un polígono, valga la redundancia, con n lados, todos con la misma longitud. Cada polígono regular tiene un radio, un apotema, un circuncírculo y un incírculo.
- En un poligono regular, el radio es aquella línea que une el medio de la figura con alguno de sus propios vértices.
- El circuncírculo es una circunferencia que pasa por alrededor del del polígono, que tiene como función, conectar todos los vértices. El radio del polígono es también el radio de la circunferencia.
- El incírculo se encuentra dentro del polígono, y es aquel que toca todos los puntos medios de cada lado. Tiene forma de círculo.
¿CÓMO PODRÍAMOS CALCULAR EL APOTEMA EN UN POLÍGONO IRREGULAR?
Es simple, los polígonos irregulares no poseen apotema, ya que en esta figura geometrica no se encuentra un punto central. Es decir, los apotemas solo se aplican a polígonos regulares.
Un polígono regular de n lados siempre tiene un apotema sin importar cuántos lados tenga, además, la longitud de la apotema se puede utilizar para calcular otras características de un polígono.
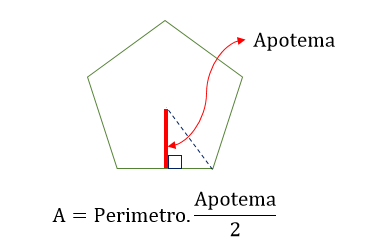
APOTEMA Y EL ÁREA
El perímetro de un polígono regular es la distancia alrededor del polígono. Si conocemos la longitud de la apotema y el perímetro de un polígono regular, podemos calcular el área del polígono usando la siguiente fórmula:
A = (1/2) aP
Aquí «a» hace referencia a la longitud y P simboliza el perímetro.
Por ejemplo, si se trata de un polígono regular de 5 lados con una longitud de apotema de 4.817 unidades y un perímetro de 35 unidades. En este caso, el área es posible resolverla sustituyendo 4.817 para «a» y 35 para P, quedaría de este modo:
A = (1/2) (4.817) (35) = 84.2975 unidades²
El área de este polígono sería de 84,2975 unidades cuadradas.
OTRAS FÓRMULAS PARA CALCULAR APOTEMAS
También se puede utilizar la fórmula del área para encontrar la apotema si se conoce tanto el área como el perímetro de un polígono.
Esto se debe a que se puede resolver para a en la fórmula, A = (1/2) aP , multiplicando ambos lados por 2 y dividiendo por P para obtener 2 A / P = a .
Viendo el ejemplo del polígono de 5 lados, se puede suponer que el área es de 84,2975 Unidades² y el perímetro es de 35 unidades.
Cuando se conectan estos números en la fórmula de la apotema, se puede obtener que:
a = 2 (84.2975) / 35 = 4.817 unidades
Cómo podemos observar, el resultado de la longitud de la apotema es de 4.817 unidades.
A veces, no se conoce el área o el perímetro de un polígono regular de n lados. Cuando este es el caso, se tiene una fórmula que se puede usar para encontrar la longitud de la apotema sabiendo solo la longitud de un lado de un polígono.
Cuando sólo se sabe la longitud de un lado, se llama es de un n -sided polígono regular, y puede usar la siguiente fórmula:
a = s / (2tan (180 / n ))
¿CÓMO CALCULAR LA APOTEMA DE UN POLÍGONO?
Un polígono es figura geometría que posee lados rectos, puede ser rectángulo, un hexágono o un cuadrado.
Se puede calcular la apotema si se conoce el área. Con el área y las longitudes de los lados, se puede usar una fórmula más simple.
EJEMPLOS: CONOCIENDO EL ÁREA
- Paso 1: Primero se debe contar cuántos lados tiene el polígono.
- Paso 2: Luego, se divide el área del polígono por el número de lados que tiene. Por ejemplo, si el área de un cuadrado es 36, se dividirá 36 entre 4 y se obtendrá 9.
- Paso 3: Se divide pi (π) por el número de lados del polígono. En el mismo ejemplo, se dividiría pi (π), aproximadamente 3,14, por 4, el número de lados de un cuadrado, para obtener un resultado de 0,785.
- Paso 4: Con una calculadora científica se debe calcular la tangente del resultado del Paso 3 en radianes. Debe tomar en cuenta que si se tiene la calculadora configurada en grados, arrojará un resultado incorrecto. La tangente de 0,785 seria aprox 1,0.
- Paso 5: Se divide el resultado del Paso 2 por el resultado del Paso 4. Continuando con el ejemplo, sería 9 entre 1 y el resultado aproximadamente sería 9.
- Paso 6: Para encontrar la longitud de la apotema debe calcular la raíz cuadrada del resultado del Paso 5. Dónde la raíz cuadrada de 9 es igual a 3, por lo que la longitud de la apotema es igual a 3.
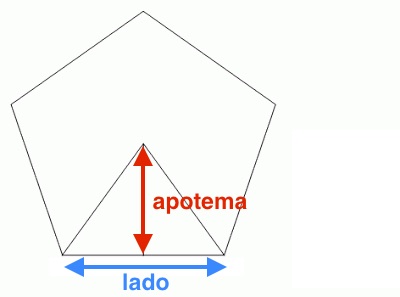
En resumen, una apotema de un polígono regular es un segmento con un punto final en el centro y el otro punto final en el punto medio de uno de los lados. Este se puede calcular mediante varias fórmulas matemáticas, dependiendo de los datos que se tengan disponibles.
