El seno ‘sen’ y el coseno ‘cos’, forman parte de las funciones o razones trigonométricas que son las relaciones entre los catetos y la hipotenusa en un triángulo rectángulo.
El seno es la razón o la división de la longitud del cateto opuesto (CO) entre la longitud de la hipotenusa (H). Mientras que el coseno es la razón entre la longitud del cateto adyacente (CA) entre la longitud de la hipotenusa (H).
Lea TAMBIÉN: QUÉ ES ALFANUMÉRICO
Un triángulo rectángulo consta de un ángulo de 90 grados y dos ángulos agudos. Cada ángulo agudo de un triángulo rectángulo tiene las funciones de seno, coseno y tangente. Tanto el seno, como el coseno y la tangente de un ángulo agudo de un triángulo rectángulo, son rezones de dos de los tres catetos de un triángulo rectángulo.
Los ángulos en las funciones trigonométricas se expresan como radianes y esto son el equivalente de los grados de los ángulos en función del radio de la circunferencia.
Etimología de la palabra seno

El astrónomo y matemático Aria Bhatta fue quien estudió el concepto de seno con el nombre de ardhá-jya,5 siendo ardhá: ‘mitad, medio’, y jya: ‘cuerda’. Luego de traducir las obras científicas al árabe, se referían a este término sánscrito como jiba .
Pero como en el árabe escrito se omiten las vocales, el término quedó abreviado jb. Escritores posteriores que no sabían el origen extranjero de la palabra creyeron que jb era la abreviatura de jiab (que quiere decir ‘bahía’, ‘cavidad’ o ‘seno’.
Más tarde a finales del siglo XII, el italiano Gerardo de Cremona tradujo los escritos del árabe al latín reemplazando el jiab por su contraparte latina sinus (‘hueco, cavidad, bahía, seno’). Luego, ese sinus se convirtió en el español ‘seno‘.
Según otra explicación, cita requerida la cuerda de un círculo, se denomina en latín inscripta corda o simplemente inscripta. La mitad de dicha cuerda se llama semis inscríptae. Su abreviatura era s. ins., que terminó simplificada como sins. Para asemejarla a una palabra conocida del latín se la denominó sinus.
Función seno y coseno
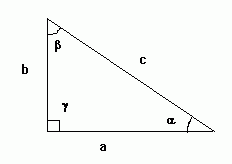
Sea un triangulo rectángulo, siendo los catetos los lados «a» y «b», y la hipotenusa el lado mayor opuesto al ángulo recto «c». Las relaciones entre los catetos y la hipotenusa se llaman seno, coseno y tangente.
Es preciso tener en cuenta que en cálculo los ángulos suelen expresarse en radianes más bien que en grados.
Ahora bien, como c > a y también c > b, se tiene que el seno y el coseno no pueden superar al valor 1; cosa que no sucede con la tangente. Además, los valores de a y b pueden ser positivos o negativos.
La tangente es un ángulo que guarda relación entre los catetos de un triángulo rectángulo. Puede expresarse como valor numérico a partir de la división entre la longitud del cateto opuesto y el cateto adyacente del ángulo en cuestión.
Mientras que el arcotangente es la función inversa de la tangente de un ángulo.
Dos o más circunferencias se consideran tangentes cuando los centros y la intersección de las circunferencias, conocida como punto de tangencia, pasan por la misma recta. Se debe dar una coincidencia de uno de los puntos de sus perímetros, de modo que sus bordes se toquen, sin que se superpongan las figuras.
Función seno
Por y = sin x (o = sen x ) se entiende la función con valores de x comprendidos entre – y + , teniendo como imágenes el seno del ángulo x radianes. Teniéndose en cuenta que si x es superior a 2 (360 grados) se considera un ángulo superior a una vuelta.
Mientras se considera a x positivo cuando partiendo de las «3 horas» ha girado en sentido contrario al normal del reloj, y se considera a x negativo cuando partiendo de esa misma posición hubiera girado en sentido del reloj.
Función coseno
Por y = cos xse entiende la función con valores de x comprendidos entre – y + , teniendo como imágenes el coseno del ángulo x radianes. También hay que tener en cuenta que si x es superior a 2 (360 grados) es considerado un ángulo superior a una vuelta.
Funciones en un círculo trigonométrico

El círculo trigonométrico es aquel cuyo radio vale la unidad. Al trazar dos ejes perpendiculares entre sí que pasan por el origen del círculo, tendremos un sistema de ejes coordenados XY.
En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, el seno será la proyección del segmento móvil sobre el eje de las ordenadas Y.
Por ejemplo si una linterna ilumina el segmento móvil dentro del círculo, la sombra que proyecta el segmento sobre el eje Y será el valor del seno.
Cuando se grafica el seno a medida que el segmento se abre, el seno crece hasta ser igual a 1, cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 180º el seno se reduce pero sigue siendo positivo.
Por encima de los 180º el seno toma valores negativos hasta llegar a los 360º. Los valores del seno se hallan entre 1 y -1.
