En matemáticas, un polinomio es un término algebraico, en donde intervienen varios números y letras, se relacionan mediante sumas, multiplicaciones y/o potencias. Las variables se escriben con las letras X o Y, pues las mismas pueden asumir diferentes valores, mientras que a los números se les denomina coeficientes.
Cada uno de los monomios del polinomio tiene un exponente distinto, el cual se denomina grado del polinomio al exponente mayor. El valor de los exponentes pertenece al conjunto N de los números naturales. Con frecuencia se suele utilizar el término polinómico como adjetivo, para nombrar cantidades las cuales se pueden expresar como polinomios de algún parámetro, ejemplo: tiempo polinómico.
Los polinomios son muy utilizados en las matemáticas y en las ciencias. Generalmente son utilizados; en cálculos y análisis matemáticos para acercar cualquier función derivable, las ecuaciones polinómicas y las funciones polinómicas se aplican en una gran variedad de problemas, desde la matemática elemental y el álgebra, hasta ámbitos como la física, química, economía y las ciencias sociales.
En álgebra abstracta, son utilizados para construir los anillos de polinomios, un concepto central en teoría de números algebraicos y geometría algebraica.
Historia de la polinomio

La resolución de igualdades algebraicas, o determinar la raíz del polinomio, se encuentra entre los problemas más antiguos de las matemáticas, sin embargo, la notación que se utiliza actualmente, se originó a partir del siglo XV.
En el problema décimo cuarto del papiro de Moscú entre las fechas ca. 1890 a.C, se solicita calcular el volumen de un tronco de pirámide cuadrangular. El escribiente expone los pasos:
- Eleva al cuadrado 2 y 4.
- Multiplica 2 por 4.
- Suma los anteriores resultados.
- Y multiplícalo por un tercio de 6 (h).
Finaliza diciendo “…ves, es 56, lo has calculado correctamente…”, en notación algebraica la forma actual sería: V = h (t² + b² + tb) / 3, lo que se traduce como un polinomio de cuatro variables (V, h, t, b), que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios como: P(x) = x² + 1, no cuentan con una raíz que sea número real, por consiguiente, si el conjunto de las raíces posibles se alarga a los números completos, todo polinomio (no constante) poseerá una raíz: este es el enunciado del teorema fundamental del álgebra.
Existe una diferencia entre la aproximación de raíces, y el descubrimiento de fórmulas concretas para ellas. Desde el siglo XVI ya se conocían fórmulas de polinomios de hasta 4to grado, sin embargo, durante muchos años, en 1824, el matemático noruego, Niels Henrik Abel, demostró que no pueden existir fórmulas generales para los no polinomios de 5to grado o mayores. Como resultado, marcó el comienzo de la teoría de Galois, la cual se ocupa del estudio, en forma detallada, de las relaciones existentes entre las raíces de los polinomios.
Composición de un polinomio

Están constituidos por un conjunto finitos de variables denominadas incógnitas, y constantes denominados coeficiente, con las operaciones aritméticas se pueden realizar: sumas, multiplicaciones y restas, así como resolver, exponentes enteros positivos pudiendo ser de una o varias variables.
Definición algebraica
Se define como expresión algebraica a un conjunto de cantidades numéricas y literales, las cuales se relacionan entre sí por los signos de las operaciones aritméticas ( “+”, “-“, “x” “/”), al igual que potencias y la extracción de raíces
Algunos ejemplos de expresiones algebraicas son:
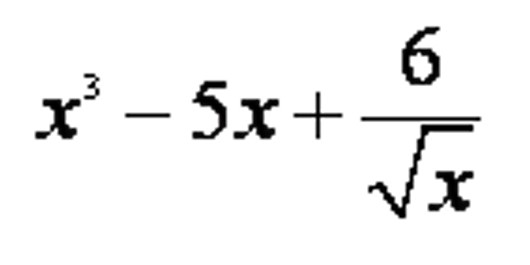
Polinomios de una indeterminada
La indeterminada, es utilizada para la definición de los polinomios con coeficientes enteros, racionales, reales o complejos. De esta manera los polinomios presentan una estructura algebraica similar a la estructura del conjunto Z de los números enteros.
- La “Variable”, cuando se trata de una “Función polinómica”, como la siguiente:
- F (X) = 3X + 5, en donde el lado derecho tiene la forma de un polinomio.
- – La “Incógnita” cuando se trata de “Ecuaciones polinómicas o Raíz de un polinomio”, tales como: 6X + 4 = 0, donde X es el número – 2/3.
Proposiciones sobre factores
Se conoce que la función: g(x) = a0xn + a1xn-1+…+an, en la cual “n” representa un número entero positivo, el cual recibe el nombre depolinomio o función racional entera de x; donde n es el grado del polinomio; los coeficientes a0, a1,…, an, representan en este caso números enteros o complejos, la variable independiente x, puede adquirir tantos valores reales o complejos. Por consiguiente, el valor de la variable x, para el cual la función es igual a 0, se denominada raíz del polinomio.
Teorema de Bezout
El resto de la división de g(x) entre x-a es igual a g(a)
Corolario: Si g(a)=0, entonces a es una raíz del polinomio.
Ejemplo: sea g(x) = x4 -5x3 + 5x2-1; como g(1) = 0,( 1 es una raíz de g.)
Teorema fundamental del álgebra: Toda función racional entera g(x) tiene al menos una raíz real o compleja
Teorema de los factores lineales
Todo polinomio de grado n, g(x) = a0xn + a1xn-1+…+an, se puede expresar como el producto de n factores lineales x-ri y por el coeficiente a0 para i=1,2,…,n.
