Una ecuación matemática puede definirse como una igualdad entre dos expresiones, donde pueden encontrarse más de una incógnita que tienen que resolverse a través de diferentes métodos. Desde la preparatoria es normal ver ecuaciones matemáticas sencillas en diferentes materias.
Una ecuación se utiliza para resolver problemas matemáticos, geométricos, físicos, químicos o de cualquier materia. Estas son muy importantes ya que se usan mucho en trabajos de investigación y para desarrollar proyectos científicos, además que también algunas son aplicadas a la vida diaria.
Las ecuaciones pueden poseer más de una incógnitas, o también que estas no posean ninguna solución o incluso que tenga más de una solución.
¿Para qué sirven las ecuaciones?

Las ecuaciones son muy importantes en el área de investigación y desarrollo de cualquier ámbito, debido a que la gran mayoría de las leyes físicas o principios están basadas en ecuaciones. Un ejemplo son las leyes de Newton o el teorema de Pitágoras, que plasmaron todos sus estudios e investigaciones a través de una ecuación.
Las ecuaciones tienen la finalidad de codificar relaciones en lenguaje algebraico, y partiendo de esto solucionarlas a través de métodos matemáticos. Son herramientas muy efectivas para poder resolver una gran cantidad de problemas.
Partes de una ecuación
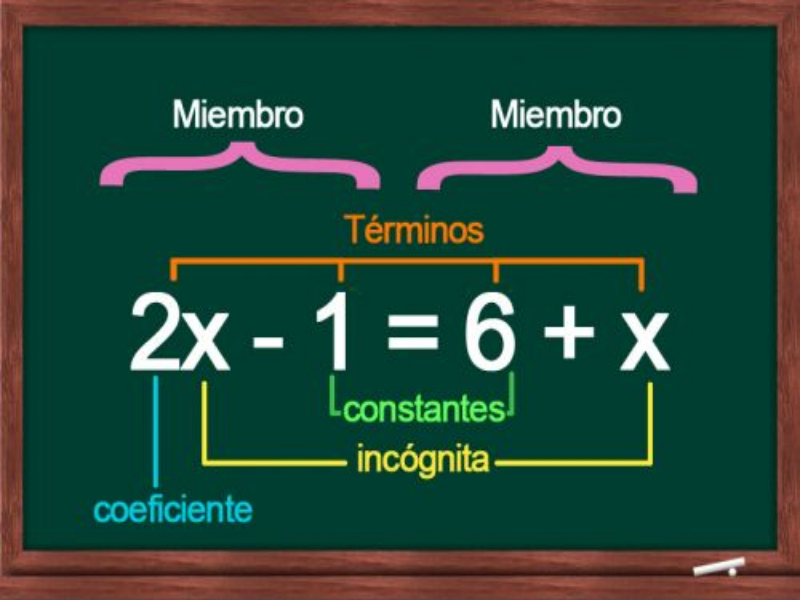
Una ecuación está conformada por varias partes. A continuación se mencionan todas estas.
- Signo igual. Una ecuación está conformado por dos extremos que son separados por un signo de igualdad (=)
- Términos. Todos los miembros están conformados por términos, estos corresponde, a todos los monomios.
- Valores. Los valores que representan una ecuación pueden ser de diferente tenor, como constantes, coeficientes, variables, funciones, vectores, entre otros.
- Incógnitas. En una ecuación puede existir más de una incógnita. Normalmente se representan con letras y son los valores que se desean encontrar.
La unión de todas estas partes da como resultado una ecuación. Donde se tienen que hacer varios métodos para poder encontrar el valor de la incógnita
Tipos de ecuaciones

Existen diferentes tipos de ecuaciones dependiendo de su función. A continuación se mostraran las más utilizadas.
Ecuaciones algebraicas
Las ecuaciones algebraicas son las más comunes de todas, se dividen en varios tipos. A continuación se mostraran algunos.
- Ecuaciones de primer grado o lineales. Son las que tienen una o más variables a la primera potencian y no representa producto entre variables. La ecuación más común es ax+b=o.
- Ecuaciones de segundo grado. En este caso la ecuación posee una incógnita elevado al cuadrado. Esto quiere decir que hay dos posibles soluciones a la ecuación. La ecuación fundamental sería ax2 + bx + c = 0.
- Ecuaciones de tercer grado. Por último se tiene una ecuación cúbica o de tercer grado, donde hay una incógnita elevada al cubo. Un ejemplo de esta seria ax3+ bx2 + cx + d = 0
Ecuaciones trascendentes
Este tipo de ecuación no puede ser resuelta a través solo utilizando operaciones algebraicas, en otras palabras la ecuación incluye una función no algebraica. Los ejemplos más comunes son funciones trigonométricas, logarítmicas y exponenciales.
Ecuaciones funcionales
En este la incógnita está en función de otra variable. Estas son ecuaciones muy avanzadas que es muy común verlas en estudios del nivel superior de carreras científicas, como ingenierías o ciencias puras.
Ecuaciones integrales
Como su nombre lo dice es la ecuación donde la incógnita está dentro de una integral. Estas normalmente se usan en problemas matemáticos complejos, o incluso para poder obtener el área y volumen de una figura.
Ecuaciones diferenciales
Por último estas son las ecuaciones que ponen en relación una función con sus derivas.
Ejemplo resuelto de una ecuación
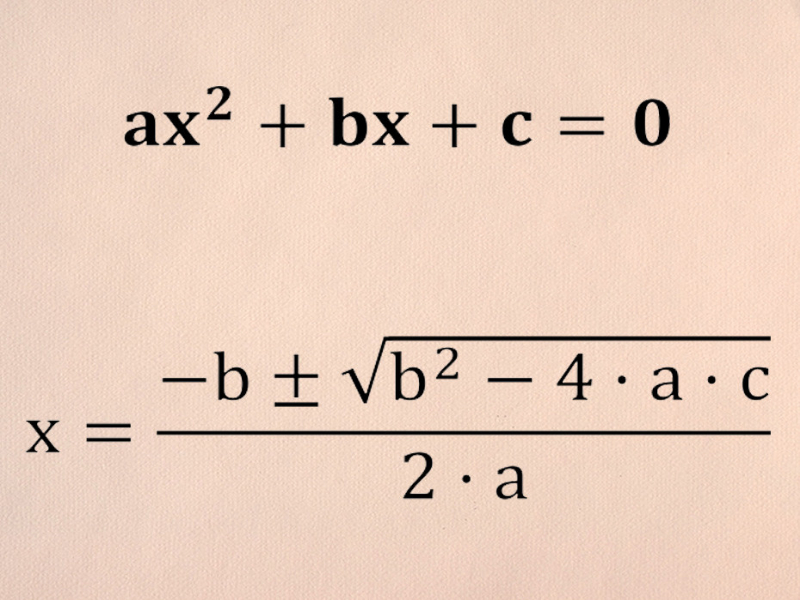
Para poder entender el concepto de una ecuación, la mejor forma de explicarlo es a través de un ejemplo. En este caso se mostrará una función muy simple
2x + 16 = 40 – 4x
Ahora para poder conseguir el valor de la incógnita es necesario despejarla. Lo primero que tendrás que hacer es agrupar los términos semejantes de un lado. En otras palabras tienes que pasar las incógnitas de un lado y las constante de otros. En ese caso la ecuación quedaría de este modo
2x + 4x = 40 – 16
Ahora lo que tienes que hacer es sumar los términos semejantes, dando como resultado
6x = 24
Por último tienes que dejar la incógnita sola para poder determinar el valor
x = 24/6
x = 4
Ecuaciones famosas
La historia está llena de muchos investigadores que plasmaron sus investigaciones a través de una ecuación matemática. Con la ayuda de esta se puede simplificar de gran medida, la solución de muchos problemas matemáticos y aritméticos. A continuación se mostraran las ecuaciones más comunes.
- Teorema de Pitágoras. Esta ecuación establece que la hipotenusa o el lado más extenso de un triángulo rectángulo serán igual a la raíz cuadrado de la suma de los dos catetos elevados al cuadrado. Esta ecuación es la base fundamental de la trigonometría
- Segunda ley de Newton. La ley de la inercia que fue estudiada por Sir Isaac Newton, establece que un objeto en reposo no cambiará de estado a menos que se le aplique una fuerza externa.
- Ley de Ohm. La ley de Ohm es la base fundamental de la electricidad. Donde se establece que la diferencia de potencial que se le aplique en los extremos de un circuito cerrado es directamente proporcional a la intensidad de corriente que cicule por el mismo.
