La palabra paralelogramo poviene del latin parallelogrammus. En la geometría se define como un polígono conformado por cuatro lados y posee la peculiaridad de que sus lados opuestos son paralelos entre sí, es decir, ambos lados se posicionan a distancias iguales. Otra característica destacable del paralelogramo es que todos sus ángulos consecutivos tienen 180 grados en total. A continuación, te explicaremos los tipos de paralelogramo, perímetro, método, ley y sus propiedades.
Tipos de paralelogramo

En el mundo de los paralelogramos existen diversas formas y tipos, los cuales se dividen en cuatro tipos:
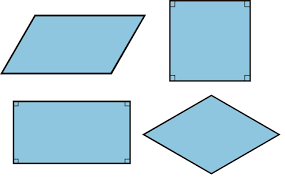
- Cuadrado: cuadrilátero cuyos lados y ángulos son iguales.
- Rectángulo: tiene los cuatro ángulos iguales (de 90º) y los lados iguales dos a dos. Sin embargo, los lados adyacentes son diferentes.
- Rombo: todos los lados son iguales pero los ángulos son diferentes dos a dos, de esta forma, los ángulos adyacentes son diferentes y cada ángulo es igual al ángulo no adyacente.
- Romboide: tiene sus lados y ángulos iguales dos a dos. El romboide también es denominado como paralelogramo no regular.
Perímetro del paralelogramo
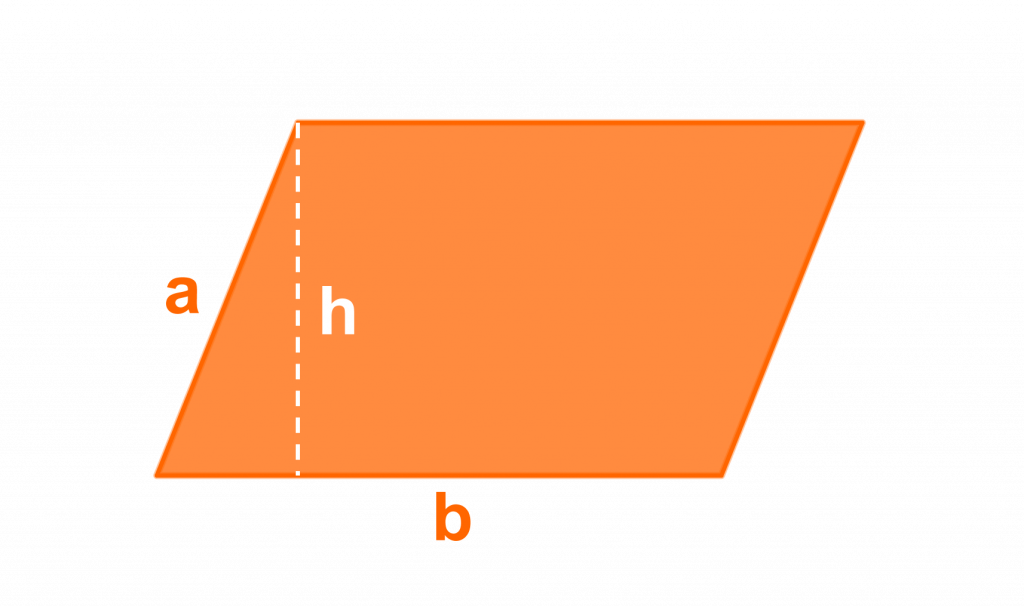
Para poder hacer los cálculos pertinentes del área de un paralelogramo, lo que debes hacer es multiplicar la altura por la base, siendo su fórmula general a = b x a. Sin embargo, si lo que estás buscando es saber el perímetro, es necesario que todos los lados que lo conforman se sumen.
Para lograr calcular el perímetro de un paralelogramo es necesario sumar la longitud de todos sus lados. Esto puedes hacerlo a través de la siguiente formula: Lado A x 2 + Lado B x 2. Por ejemplo: el perímetro de un paralelogramo rectángulo que posea dos lados opuestos de 5 centímetros y otros dos lados opuestos de 10 centímetros, se va a obtener ubicando estos valores en la ecuación antes planteada, lo que nos dará como resultado 5 x 2 + 10 x 2 = 30 centímetros.
Otra fórmula que puedes aplicar para calcular el perímetro de un paralelogramo es 2 x (Lado A + Lado B). En nuestro ejemplo: 2 x (5 + 10) = 30. Todas estas fórmulas resumen el proceso de sumar los lados que tiene cada paralelogramo. Si hacemos la operación Lado A + Lado A + Lado B + Lado B, el resultado sería el mismo (5 + 5 +10 + 10 = 30).
Ley del paralelogramo

Existe una ley conocida como ley del paralelogramo, la cual enmarca que la suma de los cuadrados de las longitudes de los cuatro lados es igual a la suma de los cuadrados de la longitud de cada diagonal. Gracias a esta ley se puede marcar la relación entre los lados que lo conforman y las diagonales del paralelogramo.
Por otro lado, el paralelogramo posee una característica particular y es que este sea un rectángulo. En ese caso, las diagonales son iguales, por lo tanto, la ley del paralelogramo queda reducida al Teorema de Pitágoras.
Propiedades diferentes del paralelogramo
En cuanto a las propiedades del paralelogramo, es necesario reunirlas en grupos, ya que muchas formas que poseen características totalmente diferentes son consideradas paralelogramos. En otras palabras, los diferentes tipos de paralelogramos poseen la particularidad de que pueden presentar propiedades peculiares, que no se puedan representar en todos por igual, como son:
- – Un paralelogramo cuadrado puede dar como resultado una figura igual si se rota en tramos de 90°, lo que también se puede establecer colocando que posee una simetría de rotación de orden 4.
- – Los paralelogramos del tipo romboide, rombo y rectángulo, deben ser rotados de a 180° para obtener el mismo resultado.
- – Un rombo tiene 2 ejes de simetría, que lo cortan juntando sus vértices opuestos.
- – Un rectángulo posee 2 ejes de simetría de reflexión que son perpendiculares a sus lados.
- – El cuadrado tiene 4 ejes de simetría de reflexión, que juntan cada par de vértices contrarios y que lo cortan por el centro vertical y de manera horizontal.
Propiedades comunes del paralelogramo
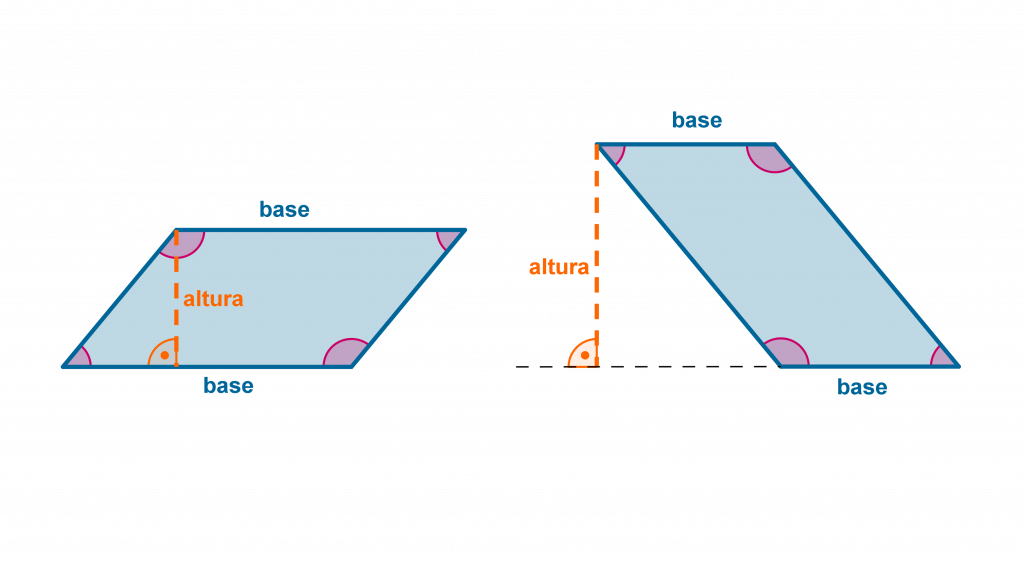
Así como existen propiedades que diferencian a los tipos de paralelogramo, también encontramos algunos puntos en común, como son:
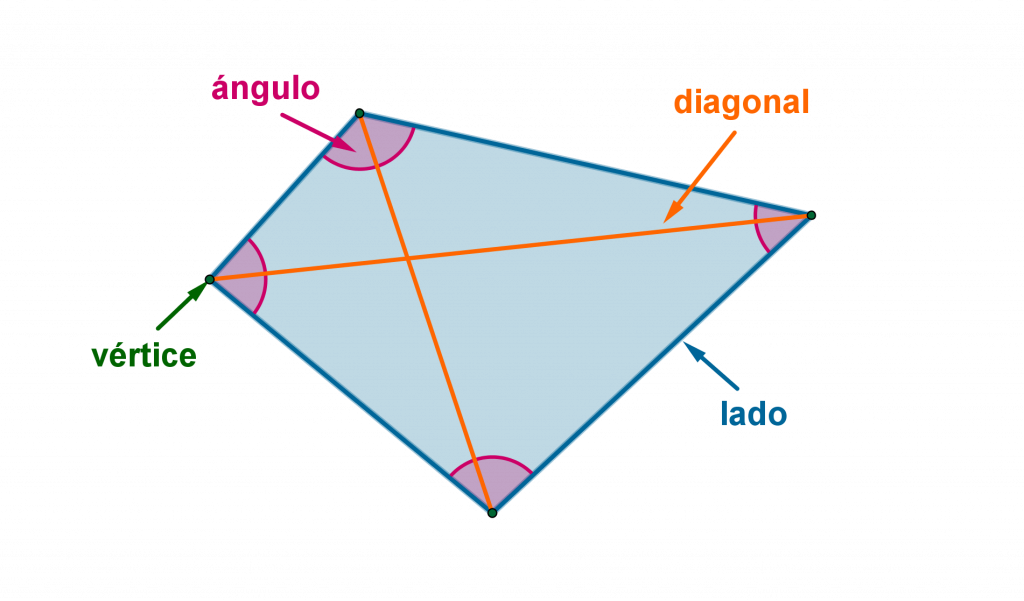
- – Podemos decir que todos los paralelogramos tienen cuatro lados y cuatro vértices, ya que forman parte del grupo de los cuadriláteros.
- – Los lados opuestos de los paralelogramos nunca se cruzan en sí, ya que siempre son paralelos.
- – Se puede decir que la longitud de los lados opuestos de los paralelogramos será siempre la misma.
- – Los ángulos opuestos del paralelogramo miden exactamente lo mismo.
- – La suma de dos de sus vértices da como resultado 180°, esto quiere decir que son suplementarios.
- – Se puede decir que los ángulos interiores deben sumar 360°.
- – Se considera que el área debe ser siempre el doble de la de un triángulo a partir de sus diagonales. Prueba a estudiar cuántos triángulos ves en esta imagen.
- – Todo paralelogramo debe considerarse como convexo.
- – Las diagonales de un paralelogramo deben bisecarse entre sí siempre.
- -Si trazamos una recta que cruce su centro el área del paralelogramo se debe dividir en dos partes idénticas.
Método del paralelogramo
Existe un método del paralelogramo que se considera un procedimiento gráfico simple que nos ayuda a hallar la suma de dos vectores.
Lo primero que debes hacer es realizar el dibujo de ambos vectores (a y b) a escala, con el punto de aplicación común.
Luego, debes completar un paralelogramo, realizando el dibujo de dos segmentos paralelos a ellos.
Finalmente, el vector suma resultante (a + b) será la diagonal del paralelogramo con origen común a los dos vectores originales mencionados anteriormente.
Para concluir, podemos decir que en la vida diaria, es muy probable que las personas se encuentren muy seguido con este tipo de figuras, ya que existen millones de objetos que pueden tener dichas formas mencionadas, bien sea un cuaderno o libro, una regla, escritorio o mesa, una tabla, entre otros varios.
No se pueden limitar los paralelogramos ni los polígonos a una ciencia específica, ya que existen muchos ámbitos y estudios en los que es necesario el uso de este tipo de figuras, de hecho hay graffitis tan realistas que parecen salirse de las paredes que los usan, como también en el campo de la ingeniería, arquitectura, carpintería, dibujo, diseño, entre otros.
